Модель объекта
| Модель – аналог или заместитель реального объекта.
| Моделирование – способ познания объектов окружающего мира.
Модель призвана отражать признаки и особенности объекта.
Выделяют два типа моделей:
» натурные (материальные) – модели, копирующие признаки оригинала;
» информационные – модели, описывающие признаки оригинала, средствами языка кодирования.
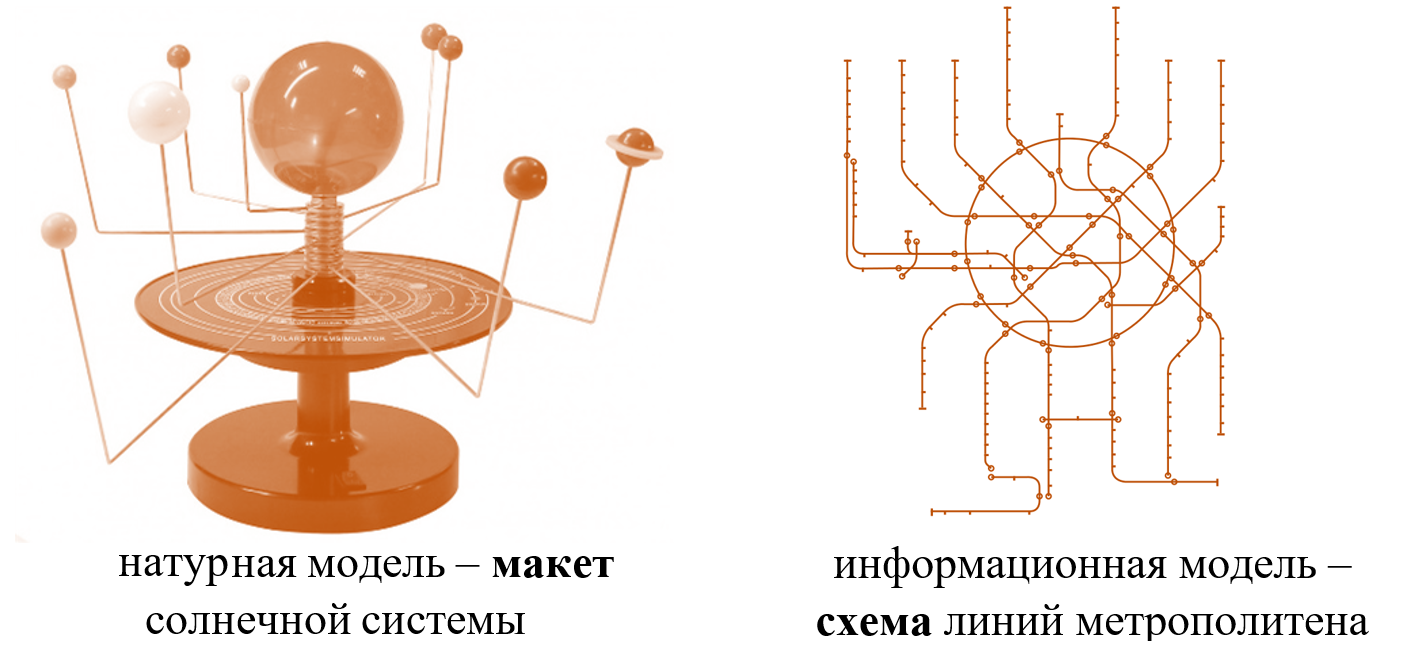
Разнообразие информационных моделей
Оригинальный объект можно заменить информационной моделью, описав его признаки.

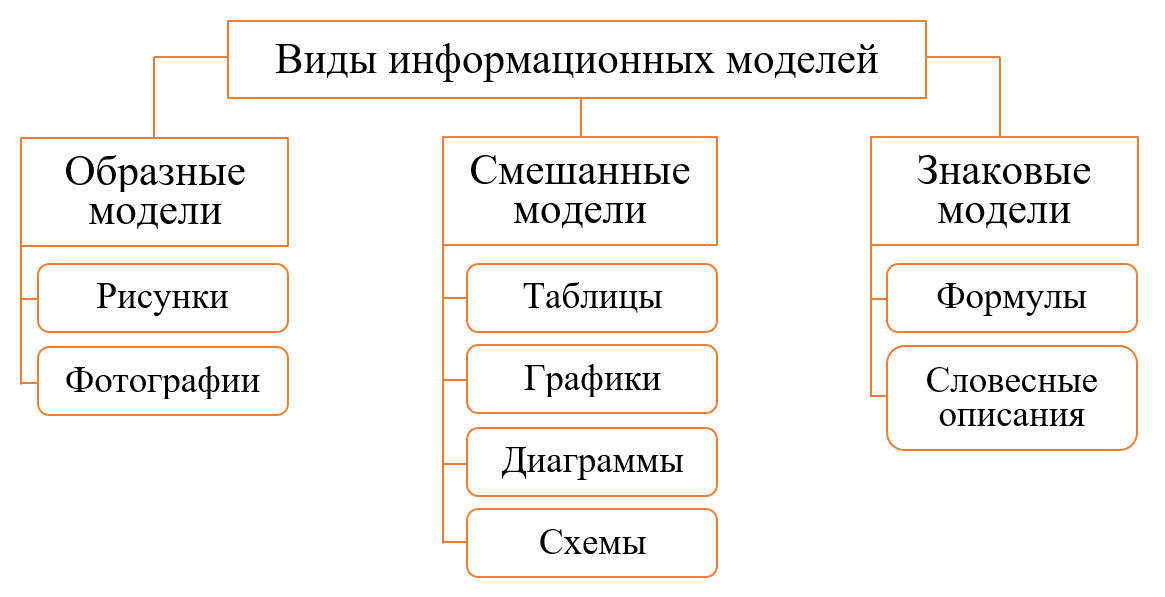
Виды алгоритмов
Подобно конструктору, алгоритмы составляют из базовых элементов.
Выделяют три типа алгоритма:
» линейный;
» разветвляющийся;
» циклический.
Такие алгоритмы удобно иллюстрировать с помощью блок-схем.
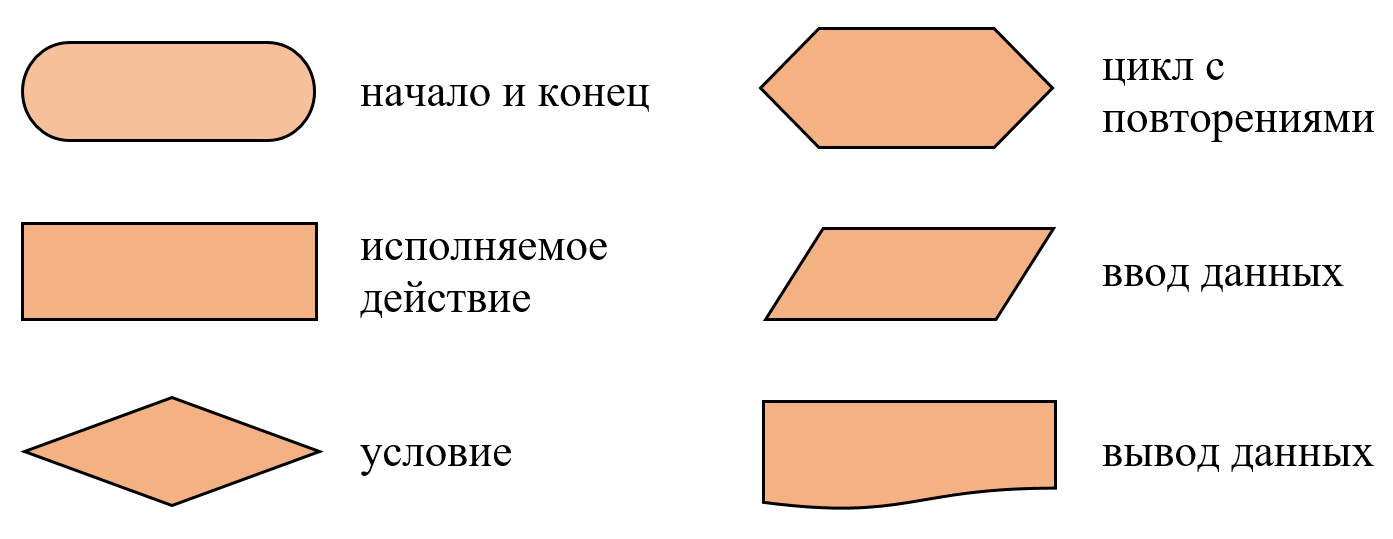
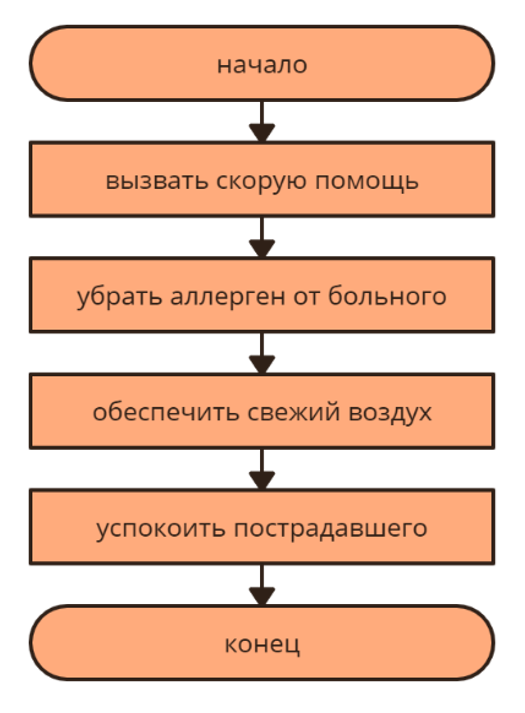
| Линейный алгоритм (последовательный) – это алгоритм, в котором все действия выполняются однократно, друг за другом.
Пример: Алгоритм «Первая помощь при отеке Квинке»
1) вызвать скорую помощь;
2) убрать аллерген от больного;
3) обеспечить приток свежего воздуха;
4) успокоить пострадавшего.
| Разветвляющийся алгоритм (условный) – это алгоритм, в котором в зависимости от условий выполняется некоторая последовательность действий.
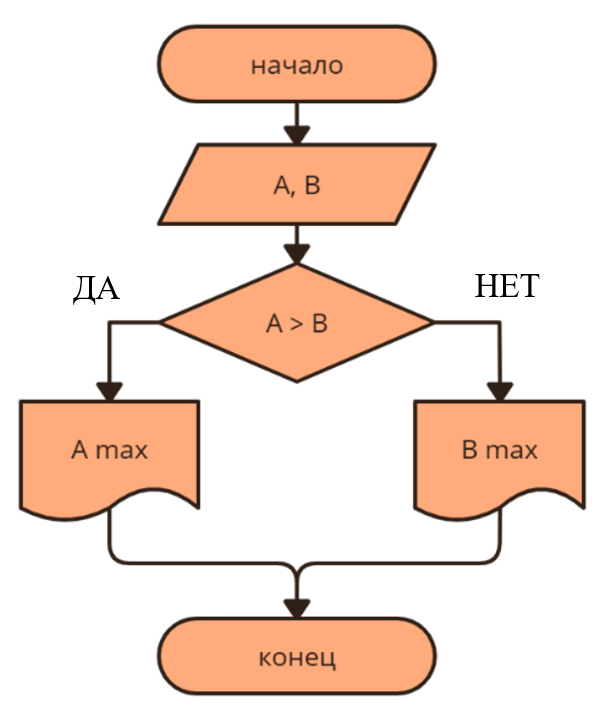
Пример: Алгоритм нахождения максимума двух чисел
1) получить два числа;
2) сравнить числа;
3) найти максимум.
| Циклический алгоритм – это алгоритм, содержащий повторяющиеся действия.
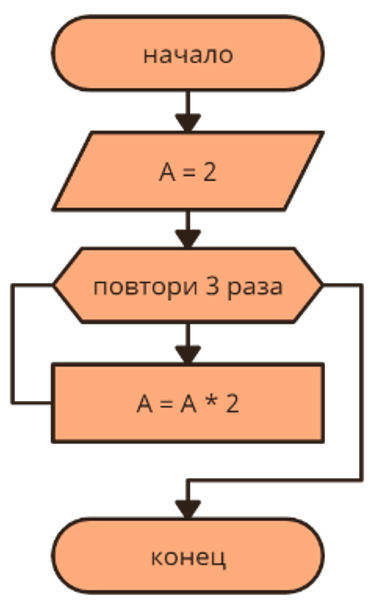
Пример: Алгоритм возведения 2 в степень 4
1) получить число 2;
2) умножить число на 2;
3) результат умножить на 2;
4) результат умножить на 2.
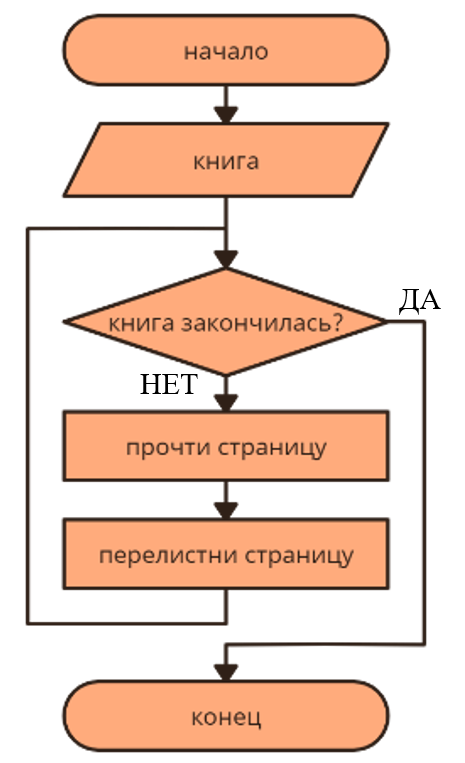
Пример: Алгоритм чтения книги
1) взять книгу;
2) пока не закончилась книга:
а) прочти страницу;
б) перелистни страницу.
Литература:
1. Информатика: учебник для 6 класса / Л.Л. Босова, А.Ю. Босова. - М.: БИНОМ.Лаборатория знаний, 2016. - 244 с.
Задачи на диаграммы Эйлер-Венна.
Задача №1.
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. Сколько шестиклассников являются читателями обеих библиотек?
Решение:
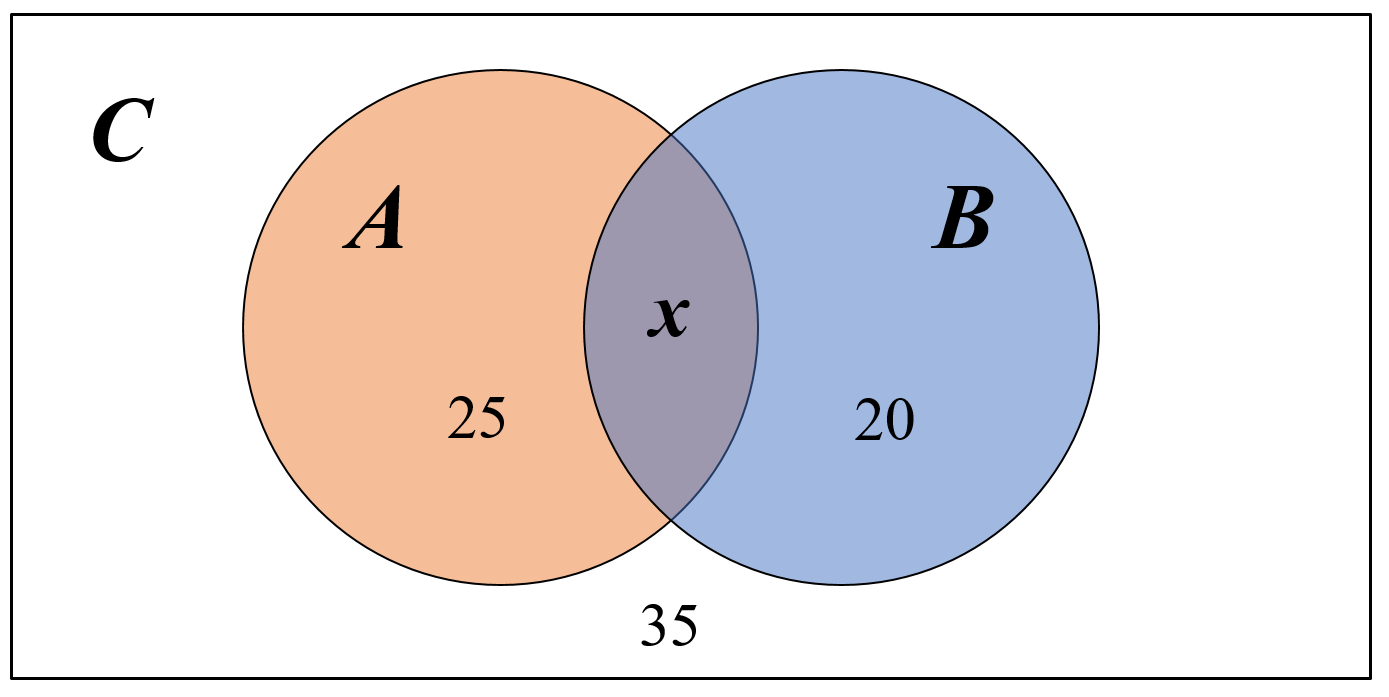
А– посещающие школьную библиотеку (25);
B– посещающие районную библиотеку (20);
С– общее количество шестиклассников (35);
Обозначим за x – количество шестиклассников, посещающих обе библиотеке.
25 + 20 – х = 35
45 – х = 35
х = 45 – 35
х = 10
Ответ: 10 человек являются читателями обоих библиотеки.
Задача №2.
В классе 25 учащихся. Из них 5 человек не умеют играть на в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 – в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?
Задача №3.
В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
а) пересечении;
б) объединении?
Задача №4.
Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский изучают 25 человек, французский – 27 человек, а тот и другой 18 человек. Сколько всего учеников в классе?
Задача №5.
В детском саду 52 ребёнка. Каждый из них любит либо пирожное, либо мороженое, либо и то и другое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любят мороженое?
Задача №6.
В классе 35 учеников, каждый из них любит футбол, волейбол или баскетбол, а некоторые – два или даже три из этих видов спорта. 24 ученика любят футбол, 18 – волейбол, 12 баскетбол. При этом 10 учеников одновременно любят футбол и волейбол, 8 – футбол и баскетбол, а 5 – волейбол и баскетбол. Сколько учеников этого класса любят все три вида спорта.
