Всероссийская олимпиада школьников
школьный этап
№1.1.
В пятизначном числе не меньше трёх цифр, которые меньше 7 и не меньше трёх нечётных цифр. Найдите самое большое из таких чисел.
В ответе нужно записать найденное число.
Чтобы число получилось максимально большим, выпишем в начало две девятки. Осталось три цифры, причём все они должны быть меньше 7. Мы не можем взять все цифры равные 6, потому что должна быть ещё одна нечётная цифра. Вместо одной шестёрки нужно взять пятёрку. Запишем цифры по невозрастанию.
Ответ: 99665
школьный этап
№1.2.
Гена утверждает, что на то, чтобы построить Дом дружбы, им потребуется больше 10 дней, а Чебурашка считает, что больше 9 дней. Сколько дней требуется на построение Дома дружбы, если известно, что один из них прав, а другой ошибается?
Ответ: 10 дней.
школьный этап
№1.3.
Три брата – Ваня, Саша и Коля – учились в разных классах одной школы. Ваня был не старше Коли, а Саша – не старше Вани. Напишите имена братьев в порядке убывания их возрастов.
Ответ: Коля, Ваня, Саша.
школьный этап
№1.4.
В доме девять этажей, но лифт сломался, и теперь в нём работают только две кнопки. Нажатие на первую кнопку приводит к тому, что лифт поднимается на пять этажей вверх, а при нажатии на вторую кнопку лифт спускается на три этажа вниз. Подниматься выше девятого этажа или спускаться ниже первого этажа нельзя, ходить по лестнице тоже нельзя. Как подняться с первого этажа на девятый?
Нужно подняться на 8 этажей, если выполнили x операций «подняться на 5», и y операций «спуститься на 3», то 5x-3y=8. Решение можно найти подбором, например, такое: y = 4, x = 4. Можно также заметить, что выполнение операции «подняться на 5» и операции «спуститься на 3» приводит к подъему на 2 этажа, поэтому эти операции нужно выполнить по 4 раза.
Для полного решения необходимо ещё привести пример последовательности операций.
| Операция | Этаж |
|---|---|
| 1 | |
| Подняться на 5 | 6 |
| Спуститься на 3 | 3 |
| Подняться на 5 | 8 |
| Спуститься на 3 | 5 |
| Спуститься на 3 | 2 |
| Подняться на 5 | 7 |
| Спуститься на 3 | 4 |
| Подняться на 5 | 9 |
школьный этап
№1.5.
Рисунки на флажках могут иметь вид круга, квадрата, треугольника или звезды, причём их можно раскрасить в зелёный, красный или синий цвет. Сколько можно сделать различных флажков?
Разложим флажки в группы по цветам. Будет три группы по четыре флажка в каждой. Всего флажков – 12.
Ответ: 12 флажков.
школьный этап
№2.1.
Таня написала на полоске бумаги подряд следующие цифры: 1 2 1 2 1 1.
После этого она склеила полоску в кольцо, то есть за последней единицей теперь идет первая единица. Затем Таня разрезала кольцо между двумя цифрами так, что развернув кольцо в полоску, получилось наименьшее число. Найдите его. В ответе нужно записать это число.
Для того, чтобы число было минимально возможным, необходимо, чтобы оно начиналось с единиц. Чем больше единиц будет в начале, тем меньше будет число. Из исходного числа можно сделать циклический сдвиг, начинающийся с трёх единиц.
Ответ: 111212.
школьный этап
№2.2.
Катя, Соня, Галя и Тамара родились 2 марта, 17 мая, 2 июля и 20 марта. Соня и Галя родились в одном месяце, а дни рождения Гали и Кати обозначаются одинаковыми числами. Назовите дату рождения каждой девочки.
Ответ: Катя — 2 июля, Соня — 20 марта, Галя — 2 марта, Тамара — 17 мая.
школьный этап
№2.3.
Женщина собрала в саду яблоки. Чтобы выйти из сада, ей пришлось пройти через четыре двери, каждую из которых охранял свирепый стражник, отбиравший половину яблок. Домой она принесла 10 яблок. Сколько яблок досталось стражникам?
После прохождения каждой двери количество яблок уменьшалось в 2 раза. Так как дверей было четыре, яблок сначала было 10·2·2·2·2 = 160. Тогда стражники забрали 160 − 10 = 150 яблок.
Ответ: 150.
школьный этап
№2.4.
В игре «Камень, ножницы, бумага» двое игроков одновременно показывают при помощи руки один из трёх условных символов – «камень», «ножницы» или «бумага». Игрок выигрывает, если он показал камень, а его противник – ножницы («камень тупит ножницы»), если он показал ножницы, а его противник – бумагу («ножницы режут бумагу»), если он показал бумагу, а его противник – камень («бумага накрывает камень»). Если два игрока показали одинаковые символы, то игра заканчивается вничью. Алёша и Боря сыграли в эту игру девять раз. Алёша два раза показал камень, три раза – ножницы, четыре раза – бумагу. Боря три раза показал камень, четыре раза – ножницы, два раза – бумагу, но порядок, в котором они показывали эти символы, неизвестен. Определите, какое наибольшее число раз мог выиграть Алёша. А какое наибольшее число раз мог выиграть Боря? Объясните свой ответ.
Составим таблицу, сколько раз каждый из мальчиков показывал каждый символ:
| Алёша | Боря | |
|---|---|---|
| Камень | 2 | 3 |
| Ножницы | 3 | 4 |
| Бумага | 4 | 2 |
Боря мог выиграть все 9 раз, если 3 раза Боря показал камень, Алёша – ножницы, 4 раза Боря показал ножницы, Алёша – бумагу, 2 раза Боря показал бумагу, Алёша – камень. Посчитаем, сколько раз Алёша мог выиграть у Бори. Такое могло произойти в следующих случаях:
1) Алёша показывает камень, Боря – ножницы. Это могло произойти не более 2 раз.
2) Алёша показывает ножницы, Боря – бумагу. Это могло произойти не более 2 раз.
3) Алёша показывает бумагу, Боря – камень. Это могло произойти не более 7 раз.
Таким образом, Алёша мог выиграть не более 7 раз. Необходимо также привести пример, когда Алёша выиграл у Бори 7 раз.
1) Алёша показывает камень, Боря показывает ножницы – 2 раза.
2) Алёша показывает ножницы, Боря показывает бумагу – 2 раза.
3) Алёша показывает бумагу, Боря показывает камень – 3 раза.
4) Алёша показывает бумагу, Боря показывает ножницы – 1 раз.
5) Алёша показывает ножницы, Боря показывает ножницы – 1 раз.
Алёша выигрывает в случаях 1-3, то есть 7 раз.
школьный этап
№2.5.
В клетки таблицы 3×3 вписаны числа от 1 до 9. Катя нашла сумму чисел в каждом из квадратов 2×2, а затем сложила полученные суммы. Какова наименьшая возможная сумма этих четырёх сумм?
Пронумеруем клетки таблицы (см. рисунок). Тогда сумма всех сумм будет равна 4 × B2 + 2 × (B1 + A2 + B3 + C2) + (A1 + C1 + A3 + C3), значит, наименьшее число нужно записать в клетку B2, а следующие четыре наименьших числа в клетки B1, A2, B3, C2. Наименьшее возможное значение в клетке B2 равно 1, а наименьшее значение суммы клеток B1, A2, B3 и C2 равно 14. Тогда наименьшее значение всей суммы 62.
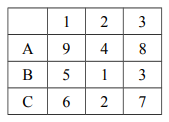
Ответ: 62.
школьный этап
№2.6.
Коля зашифровал слово, и, чтобы не забыть, написал себе подсказку. Пользуясь Колиной подсказкой, отгадайте слово. Запишите загаданное Колей слово. Укажите соответствие между буквами слова и знаками ключа.
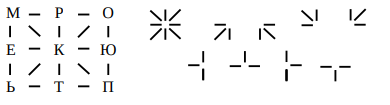
Шифр – палочки, нарисованные непосредственно вокруг буквы.
Ответ: КОМПЬЮТЕР.
школьный этап
№3.1.
Пять мальчиков: Дима, Глеб, Федя, Боря и Юра участвовали в соревнованиях по бегу. После окончания соревнований болельщики сказали об их результатах следующее:
1. Дима был не первым.
2. Глеб пришел к финишу третьим.
3. Федя пришел к финишу после Димы.
4. Юра не был последним.
5. Глеб и Федя всю дистанцию бежали рядом, и только на финише один из них вырвался вперед.
Расставьте мальчиков в том порядке, в котором они финишировали. В ответе нужно записать пять русских букв Д, Г, Ф, Б, Ю соответствующих первым буквам имён мальчиков в том порядке, в котором они финишировали. Например, запись “ДГФБЮ” означает, что первым был Дима, вторым — Глеб, третьим — Федя, четвёртым — Боря и пятым — Юра.
Глеб пришёл к финишу третьим, запишем это так: “..Г..” — поставим точки вместо неизвестных позиций. Глеб и Федя финишировали рядом по последнему условию, возможны два варианта: “.ФГ..” или “..ГФ.”. Первый вариант не возможен. т.д. Федя пришёл после Димы, но Дима был не первым, значит, остаётся вариант “..ГФ.”. Дима был не первым, но финишировал раньше Феди, поэтому “.ДГФ.”. Юра был не последним, значит, “ЮДГФ.”. Поставим Борю на оставшееся последнее место.
Ответ: ЮДГФБ.
школьный этап
№3.2.
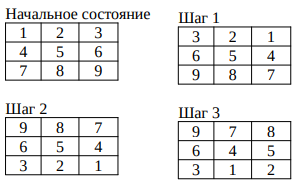
В таблице разрешается переставлять местами любые две строки друг с другом и любые два столбца. Можно ли с помощью нескольких таких операций получить из левой таблицы правую? Если да, то приведите набор операций, содержащий минимальное число операций перестановки. Если нет — то объясните почему.
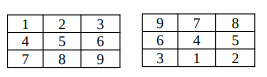
Нужный результат достигается, например, выполнением следующих команд:
Поменять столбцы 1 и 3.
Поменять строки 1 и 3.
Поменять столбцы 2 и 3.
школьный этап
№3.3.
Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до 5-й ступеньки?
Заметим, что количество способов попасть на заданную ступеньку равно сумме количества способов попасть на предыдущую ступеньку и количества способов попасть предпредыдущую ступеньку. Составим таблицу:
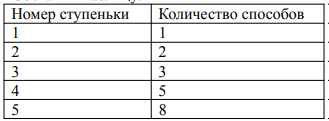
Ответ: 8.
школьный этап
№3.4.
Три вора – Камнев, Ножницын и Бумагин хотят переправиться через реку. У каждого вора два больших баула. В лодке три места, одно место занимает один человек или один баул. Грести умеет только Камнев. При этом если Камнев останется в лодке или на берегу с баулом Ножницына и Ножницына не будет рядом, то Камнев обчистит баул Ножницына. Аналогично Ножницын обчистит баул Бумагина в его отсутствие, а Бумагин обчистит баул Каменева в его отсутствие. Как им переправиться на другой берег? Опишите алгоритм их действий.
Возможный алгоритм действий.
1) Камнев перевозит два своих баула и возвращается назад.
2) Камнев перевозит Ножницына с баулом Ножницына, возвращается с Ножницыном.
3) Камнев перевозит Ножницына с баулом Ножницына, возвращается один назад.
4) Камнев перевозит Бумагина с баулом Бумагина, оставляет их на другом берегу, возвращается назад с двумя своими баулами.
5) Камнев перевозит баул Бумагина и возвращается назад.
6) Камнев перевозит два своих баула.
школьный этап
№3.5.
Вытянув репку, дед, бабка, внучка, Жучка, кошка и мышка решили отпраздновать это событие. Они хотят рассесться вокруг круглого стола и торжественно поужинать вытянутой репкой. Однако у каждого героя сказки есть свои пожелания к рассадке.
• Кошка и Жучка, как и любая кошка с собакой, хотят сидеть максимально далеко друг от друга.
• Мышке всё равно, где сидеть, лишь бы не рядом с кошкой.
• Внучка хочет сидеть непременно между бабкой и Жучкой.
• Дед хочет всё время видеть свою любимую внучку, поэтому требует, чтобы она сидела ровно напротив него.
• Бабка и дед не очень ладят в последнее время, поэтому между ними обязательно должен сидеть хотя бы один персонаж сказки.
• Бабка хочет, чтобы рядом с ней обязательно сидела кошка. Как должны рассесться герои сказки, чтобы все остались довольны?
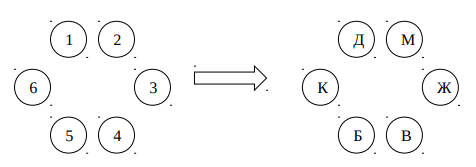
Пронумеруем места за столом от 1 до 6. По условию, дед и внучка должны сидеть напротив друг друга (пусть, например, это будут места 1 и 4). Бабка не должна сидеть рядом с дедом, поэтому её можно посадить рядом с внучкой, пусть это будет место 5. Кошка должна сидеть рядом с бабкой, значит, кошку нужно посадить на место 6. Чтобы кошка и Жучка сидели как можно дальше друг от друга, они также должны сидеть напротив, значит, Жучку нужно посадить на место 3. Оставшееся место 2 занимает мышка, при этом выполнены все условия. Ответ приведён на рисунке, это единственный возможный ответ с точностью до поворотов и отражений.
школьный этап
№3.6.
Али-Баба нашёл в пещере разбойников 9 золотых слитков. Его весы могут показать только суммарный вес двух любых слитков. Как ему узнать, сколько всего килограммов золота он нашёл, не более чем за 6 взвешиваний?
1. Пронумеруем слитки.
2. Взвесим слитки 1 и 2.
3. Взвесим слитки 2 и 3.
4. Взвесим слитки 3 и 1.
5. Сложим результаты первых трёх взвешиваний и поделим пополам. Получим суммарный вес первых трёх слитков.
6. Взвесим слитки 4 и 5.
7. Взвесим слитки 6 и 7.
8. Взвесим слитки 8 и 9.
9. Сложим результаты пунктов 5–8 и получим сумму всех найденных слитков.
школьный этап
№4.1.
На трёх путях сортировочной станции стоят вагоны с абрикосами (А), бананами (Б) и вишней (В) так, как это показано на рисунке.
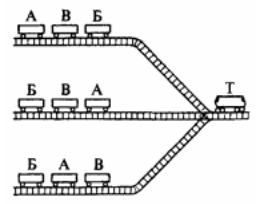
Машинист тепловоза (Т) может за один раз прицепить к тепловозу один или несколько вагонов с какого-нибудь пути, передвинуть их на правый путь, после чего передвинуть их на любой левый путь. Например, если тепловоз заберет 2 вагона с пути номер 3 на путь номер 1, то после такого действия распределение вагонов по путям будет таким.
1. А В Б А В
2. Б В А
3. Б
Соответствующую команду перемещения будем записывать так.
2 3 1
Что означает, что необходимо передвинуть 2 вагона с пути номер 3 на путь номер 1. Первое число обозначает количество перемещаемых вагонов, второе число — номер пути, с которого нужно забрать вагоны, третье число — номер пути, на который нужно передвинуть вагоны. Разработайте алгоритм действий машиниста, необходимых для того, чтобы сформировать на каждом из путей составы с одинаковыми фруктами (не важно, на каком именно пути). Алгоритм оформите в виде последовательности команд, записанных в отдельных строках. Каждая команда имеет указанный выше вид: сначала записано число передвигаемых вагонов, потом номер пути с которого передвигаются вагоны, затем номер пути, на который передвигаются вагоны.
Например, следующая запись:
2 3 1
1 2 3
означает “передвинуть 2 вагона с пути 3 на путь 1, затем передвинуть 1 вагон с пути 2 на путь 3”. Чем меньше команд будет в вашем алгоритме, тем большее количество баллов вы получите.
Самое короткое решение состоит из 7 команд:
2 1 3
4 3 2
5 2 1
3 1 2
1 3 2
5 2 3
2 3 2
Это решение оценивается в 10 баллов. Более длинные решения оцениваются меньшим числом баллов.
школьный этап
№4.2.
На берегу бурной реки встретились горилла с двумя детьми и шимпанзе с двумя детьми. К берегу прибилось бревно, которое вмещает только двух обезьян, но, во-первых, управлять бревном могут только взрослые особи, а во-вторых, если на бревне или на берегу горилл будет больше, чем шимпанзе, то они их съедят. Как всем обезьянам благополучно переправиться? Запишите алгоритм переправы.
Введём обозначения:
Горилла – взрослая горилла; горилла1 – первый ребенок гориллы, горилла2 – второй ребенок гориллы.
Шимпанзе – взрослая шимпанзе; шимпанзе1 – первый ребенок шимпанзе, шимпанзе2 – второй ребенок шимпанзе.
Алгоритм:
1. Переправить Горилла и горилла1
2. Переправить Горилла
3. Переправить Горилла и горилла2
4. Переправить Горилла
5. Переправить Шимпанзе и шимпанзе1
6. Переправить Шимпанзе и горилла2
7. Переправить Шимпанзе и Горилла
8. Переправить Шимпанзе и горилла1
9. Переправить Шимпанзе и шимпанзе2
10. Переправить Горилла
11. Переправить Горилла и горилла1
12. Переправить Горилла
13. Переправить Горилла и горилла2
школьный этап
№4.3.
Семья рыбаков (отец и сын) хочет переправить боевую группу из 6 бойцов на Тайный остров архипелага в тылу врага. Есть двухместная лодка. Не запомнив дороги, без проводника её не проплыть. Вначале дорогу до Тайного острова знает только рыбак-отец. Но всех проводить он не сможет: путь лежит мимо Сторожевой башни, и каждый из них может проплыть мимо неё не более 5 раз в любом направлении (иначе поднимется тревога). Остальные могут стать проводниками, запомнив дорогу. Рыбак-сын запоминает дорогу, если проплыл по ней один раз, а бойцу для этого надо проплыть туда и обратно. В конце все рыбаки должны быть дома, все бойцы – на острове, лодка – где угодно. Запишите алгоритм переправы.
1. Переправить Отца и Бойца 1.
2. Отец и Боец 1 возвращаются (Боец 1 запомнил дорогу).
3. Переправить Отца и Сына (Сын запомнил дорогу).
4. Отец возвращается.
5. Переправить Бойца 1 и Бойца 2.
6. Сын и Боец 2 возвращаются (Боец 2 запомнил дорогу).
7. Переправить Сына и Бойца 3.
8. Сын возвращается.
9. Переправить Бойца 2 и Бойца 4.
10. Боец 2 возвращается.
11. Переправить Бойца 2 и Бойца 5
12. Боец 1 возвращается
13. Переправить Бойца 1 и Бойца 6.
школьный этап
№4.4.
Есть чашечные весы без делений. Для взвешивания груза также можно использовать гирьки, массы которых – целое число граммов. Вам необходимо предложить набор гирек, при помощи которого можно отмерить на весах любую массу, равную целому числу граммов от 1 до 10, при этом число гирек в наборе должно быть как можно меньше. Гирьки можно класть на каждую чашку весов, чашки весов должны находиться в равновесии, при этом на одной из чашек весов должен находиться взвешиваемый груз. Массы гирек в наборе могут повторяться. Объясните, как любую массу от 1 до 10 граммов можно взвесить при помощи предложенного набора.
В оптимальном наборе гирек для уравновешивания любых масс необходимо использовать гирьки, массы которых являются степенями тройки: 1, 3, 9, 27 и т. д. Это связано с тем, что любое число можно представить в уравновешенной троичной системе счисления, при этом цифра 1 будет соответствовать тому, что гирька данной массы кладётся на одну чашку весов, цифра −1 будет соответствовать гирьке на другой чашке весов, а 0 означает, что данная гирька не используется.
Приведем пример уравновешивания всех масс от 1 до 10 при помощи гирек массами 1, 3, 9.
1 = 1.
2 = 3 − 1,
3 = 3,
4 = 3 + 1,
5 = 9 − 3 − 1,
6 = 9 − 3,
7 = 9 − 3 + 1,
8 = 9 − 1,
9 = 9,
10 = 9 + 1.
От учащегося требуется привести пример конструкции из трёх гирек (их массы могут отличаться от примера 1, 3, 9) и показать, что любую массу можно уравновесить при помощи данного набора гирек.
школьный этап
№4.5.
К реке подошли Волчица с двумя волчатами и Лисица с двумя лисятами. У берега привязана лодка, которая вмещает только двух зверей. Ситуация осложняется тем, что Волчица с Лисицей не доверяют друг другу и не оставят своих детей в своё отсутствие с другой мамой ни на берегу, ни в лодке. Грести умеют только Лисица и один из лисят. Как им переправиться?
Обозначим лисенка, который умеет грести как «лисенок1». Возможный план перевозки.
1. Перевезти лисенка1 и лисенка.
2. Перевезти лесенка1
3. Перевезти Лисицу и лисенка1
4. Перевезти Лисицу
5. Перевезти Лисицу и Волчицу
6. Перевезти лисенка1
7. Перевезти лисенка1 и волчонка
8. Перевезти лисенка1
9. Перевезти лисенка1 и волчонка
школьный этап
№4.6.
Двум англичанам, путешествующим в джунглях Африки, и двум их проводникам из местного племени требуется переправиться на противоположный берег реки. В распоряжении путешественников имеется небольшая надувная лодка, способная вместить только двух человек. Англичане подозревают, что проводники — из племени людоедов, и чувствуют себя в опасности всегда, когда находятся в меньшинстве. Как устроить безопасную переправу?
Возможный план перевозки:
1. Перевезти двух проводников.
2. Один проводник возвращается.
3. Перевезти двух англичан.
4. Другой проводник возвращается.
5. Перевезти двух проводников.
школьный этап
№5.1.
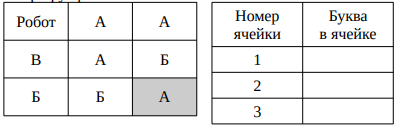
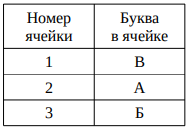
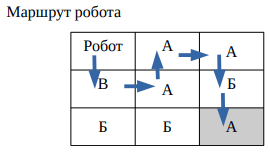
Робот стоит на поле 3×3 в левой верхней клетке. В остальных клетках поля записаны буквы A, Б, В (см. рисунок). Робот умеет шагать в соседнюю клетку только по вертикали или по горизонтали. Покидая клетку, робот стирает записанную в ней букву. У робота есть память из трёх пронумерованных по порядку ячеек (см. рисунок справа). Каждая ячейка содержит одну из букв А–В. Буквы в ячейках не повторяются.
Очередной шаг робот выполняет по следующим правилам:
• Робот не шагает в клетку, буква в которой была стёрта.
• Робот просматривает свою память последовательно, начиная с ячейки под номером 1. Если робот находит ячейку, в которой записана буква, также записанная в одной из соседних с роботом клеток, робот перемещается в эту клетку (робот использует подходящую ячейку программы с минимальным номером).
• Если робот нашёл такую ячейку, что буква в этой ячейке записана в двух и более соседних с роботом клетках, то он ломается.
• Если робот не нашёл ни одной подходящей ячейки, то он ломается. Останавливается робот, когда достигает правой нижней клетки. Заполните ячейки памяти робота так, чтобы робот пришёл в правый нижний угол поля и постройте маршрут робота.
школьный этап
№5.2.
Роджеру Вилко надо попасть в серверную космолёта «Аркада». Для этого надо пройти через комнату с горячим полом, находиться в которой человеку небезопасно. На другом конце комнаты (в правом верхнем углу) есть кнопка, отключающая подогрев пола. К счастью, у Роджера есть робот с программным управлением. У робота есть поле для программы (5 ячеек). В каждой ячейке можно записать только одну из следующих команд:
С – продвинуться на одну плитку на север (вверх);
Ю – продвинуться на одну плитку на юг (вниз);
З – продвинуться на одну плитку на запад (влево);
В – продвинуться на одну плитку на восток (вправо).
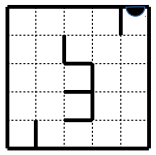
Если робот не может выполнить команду, написанную в ячейке, он просто пропускает её. Если робот выполнил все команды из своей программы, он начинает выполнять её заново. В комнате расставлены шкафы, которые роботу приходится обходить. Если робот уткнётся в стену с кнопкой (то есть совершит движение в направлении стены), он автоматически её нажимает. У Роджера есть чертёж комнаты. Помогите Роджеру запрограммировать робота так, чтобы подогрев пола был отключён. Начальное положение – робот находится в левом нижнем углу комнаты. Укажите правильный ответ и нарисуйте маршрут передвижения робота.
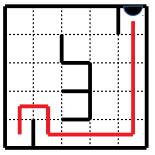
Ответ: СВЮВС.
школьный этап
№5.3.
Вам нужно умножить некоторое большое число X на 15. У вас есть калькулятор, но на калькуляторе сломались все кнопки операций, кроме сложения. Поэтому вы можете только складывать разные числа (например, можно сложить число X и число X, тогда получится 2X, затем можно сложить число 2X и 2X и получится 4X, а можно сложить 2X и X и получится 3X, то есть можно складывать любые ранее полученные числа между собой). Определите, при помощи какого минимального числа сложений можно получить число 15X. Приведите последовательность операций, при помощи которых можно получить число 15X за указанное число сложений.
Задачу можно решить за пять операций. Например:
1) 2X = X + X.
2) 3X = 2X + X.
3) 6X = 3X + 3X.
4) 12X = 6X + 6X.
5) 15X = 12X + 3X.
школьный этап
№5.4.
Серёжа, Костя и Женя решили помочь малышам построить замок из цветных кубиков. Кубиков всего девять: три красных, три жёлтых и три синих. Замок состоит из трёх башен следующей формы и цветов.
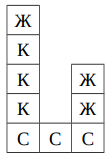
Мальчики договорились, что в их бригаде каждый может ставить только кубики одного цвета: Серёжа ставит синие кубики, Костя – красные, Женя – жёлтые. Каждую секунду каждый из мальчиков может выполнить только одно из трёх действий.
• Взять кубик.
• Поставить кубик на место.
• Ничего не делать.
При этом одновременно мальчики не могут ставить кубики в одну и ту же башню. Сколько секунд понадобится Серёже, Косте и Жене, чтобы построить замок? Запишите алгоритм их действий.
Запишем решение в виде таблицы, в которой указаны действия каждого мальчика в каждую секунду. Запись «+С» означает, что мальчик берёт в руку синий кубик, запись «С1», «С2», «С3» означает, что мальчик ставит синий кубик в первую, вторую или третью башню. Буква «К» обозначает красный цвет, «Ж» – жёлтый. Наилучшее решение возможно за 9 секунд.
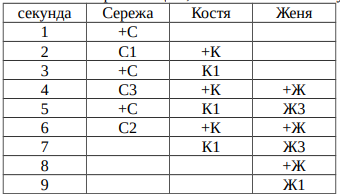
Другие решения требуют большего времени. В приведённом выше решении используется «оптимизация» – когда один мальчик кладёт кубик, то другой одновременно берёт кубик в руку и кладёт его в следующую секунду. Это позволяет положить два первых кубика в первую башню за три секунды. Если не использовать такую оптимизацию, то есть если мальчики одновременно берут кубики в руку на нечётных секундах и ставят кубики в башни на чётных секундах, то решение возможно только за 10 секунд.
школьный этап
№5.5.
Роботу нужно добраться из левого верхнего угла квадрата 4×4 в правый нижний угол. У него всего две команды: вправо (робот перемещается вправо на одну клетку) и вниз (робот перемещается вниз на одну клетку). У этой задачи много решений, например, можно перемещаться так: вправо, вправо, вправо, вниз, вниз, вниз. Поставьте на поле стенки между некоторыми клетками, чтобы решить задачу можно было ровно десятью способами. Объясните, почему в предложенном вами решении будет ровно 10 способов.

Например, поставить стенку вдоль одной из стенок почти до упора. Получится прямоугольник 3×4, а его можно пройти десятью способами, так как это число сочетаний из 5 по 3: всего 5 команд в программе для робота, из них команда вправо может быть на трёх местах, порядок неважен. Подсчёт числа маршрутов может быть выполнен разными способами – полным перебором, или как указано ниже или при помощи каких-либо иных соображений.
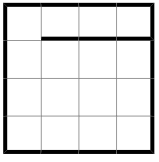
Задача допускает различные решения. Для проверки числа маршрутов таблица заполняется числами от левого верхнего угла, обозначающими число маршрутов из левой верхней клетки в данную. Затем в каждую клетку вписывается сумма чисел, стоящих слева и сверху от данной клетки, если между этими клетками нет стенки. При наличии стенки на границе с одной из соседних клеток слева или сверху – вместо суммы вписывается число, стоящее в той соседней клетке, которая не отделена стенкой. Пример заполнения таблицы для приведённого ответа:
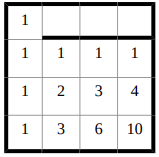
школьный этап
№1.1.
Катя, Соня, Галя и Тамара родились 2 марта, 17 мая, 2 июля и 20 марта. Соня и Галя родились в одном месяце, а дни рождения Гали и Кати обозначаются одинаковыми числами. Назовите дату рождения каждой девочки.
Ответ: Катя — 2 июля, Соня — 20 марта, Галя — 2 марта, Тамара — 17 мая.
школьный этап
№1.2.
Для групповых операций с файлами используются маски имён файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов. Также в маске может встречаться символ “*”, обозначающий любую последовательность любых символов, возможно пустую. Например, если задана маска “a*po*”, то такой маске удовлетворяют файлы с именами “airport”, “appoint’, “apologize”, но не удовлетворяют, например, файлы с именами “approve”; или “weapon”.
Вам нужно придумать маску имени файла, которой удовлетворяли бы следующие имена файлов:
python_program
и
math_theorem
но при этом НЕ удовлетворяли бы файлы с именами
nuclear_synthesis
и
biological_system
Вам нужно придумать как можно более короткую маску (содержащую как можно меньше символов). Чем короче будет придуманная вами маска, тем больше баллов вы получите.
Ответом на эту задачу является строка, которая может содержать строчные буквы английского алфавита, символ “_” (подчёркивание) и символ “*” (звёздочка).
Строки python_program и math_theorem заканчиваются на одну и ту же букву “m”. Поэтому рассмотрим маску, заканчивающуюся на “*m”. nuclear_synthesis уже не подходит под эту маску, осталось выбрать в первых двух именах такую общую букву, которой нет в имени biological_system. Например, такой буквой является “h”, поэтому “*h*m” — подходящая маска.
Составить маску из трёх букв нельзя, например, если рассмотреть маску вида “*z*”, где “z” — какая-то буква, то эта буква должна встречаться в первых двух именах, но не должна встречаться в двух других именах. Такой буквы нет.
Ответ: *h*m.
школьный этап
№1.3.
Три брата – Ваня, Саша и Коля – учились в разных классах одной школы. Ваня был не старше Коли, а Саша – не старше Вани. Напишите имена братьев в порядке убывания их возрастов.
Ответ: Коля, Ваня, Саша.
школьный этап
№1.4.
В доме девять этажей, но лифт сломался, и теперь в нём работают только две кнопки. Нажатие на первую кнопку приводит к тому, что лифт поднимается на пять этажей вверх, а при нажатии на вторую кнопку лифт спускается на три этажа вниз. Подниматься выше девятого этажа или спускаться ниже первого этажа нельзя, ходить по лестнице тоже нельзя. Как подняться с первого этажа на девятый?
Нужно подняться на 8 этажей, если выполнили x операций «подняться на 5», и y операций «спуститься на 3», то 5x-3y=8. Решение можно найти подбором, например, такое: y = 4, x = 4. Можно также заметить, что выполнение операции «подняться на 5» и операции «спуститься на 3» приводит к подъему на 2 этажа, поэтому эти операции нужно выполнить по 4 раза.
Для полного решения необходимо ещё привести пример последовательности операций.
| Операция | Этаж |
|---|---|
| 1 | |
| Подняться на 5 | 6 |
| Спуститься на 3 | 3 |
| Подняться на 5 | 8 |
| Спуститься на 3 | 5 |
| Спуститься на 3 | 2 |
| Подняться на 5 | 7 |
| Спуститься на 3 | 4 |
| Подняться на 5 | 9 |
школьный этап
№1.5.
В клетки таблицы 3×3 вписаны числа от 1 до 9. Катя нашла сумму чисел в каждом из квадратов 2×2, а затем сложила полученные суммы. Какова наименьшая возможная сумма этих четырёх сумм?
Пронумеруем клетки таблицы (см. рисунок). Тогда сумма всех сумм будет равна 4 × B2 + 2 × (B1 + A2 + B3 + C2) + (A1 + C1 + A3 + C3), значит, наименьшее число нужно записать в клетку B2, а следующие четыре наименьших числа в клетки B1, A2, B3, C2. Наименьшее возможное значение в клетке B2 равно 1, а наименьшее значение суммы клеток B1, A2, B3 и C2 равно 14. Тогда наименьшее значение всей суммы 62.

Ответ: 62.
школьный этап
№1.6.
Коля зашифровал слово, и, чтобы не забыть, написал себе подсказку. Пользуясь Колиной подсказкой, отгадайте слово. Запишите загаданное Колей слово. Укажите соответствие между буквами слова и знаками ключа.
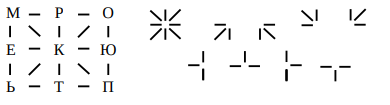
Шифр – палочки, нарисованные непосредственно вокруг буквы.
Ответ: КОМПЬЮТЕР.
школьный этап
№2.1.
В таблице разрешается переставлять местами любые две строки друг с другом и любые два столбца. Можно ли с помощью нескольких таких операций получить из левой таблицы правую? Если да, то приведите набор операций, содержащий минимальное число операций перестановки. Если нет — то объясните почему.

Нужный результат достигается, например, выполнением следующих команд:
Поменять столбцы 1 и 3.
Поменять строки 1 и 3.
Поменять столбцы 2 и 3.

школьный этап
№2.2.
Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до 5-й ступеньки?
Заметим, что количество способов попасть на заданную ступеньку равно сумме количества способов попасть на предыдущую ступеньку и количества способов попасть предпредыдущую ступеньку. Составим таблицу:

Ответ: 8.
школьный этап
№2.3.
План города представляет собой прямоугольник размером n×m километров, разбитых на кварталы — квадраты со стороной 1 километр. Между кварталами, а также по границе города проложены дороги. Например, если n = 2, m = 3, то план дорог следующий.
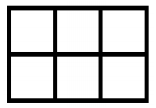
Определите суммарную длину всех дорог в городе в километрах. Единицу измерения указыватьне нужно.
Ответом к этой задаче является некоторое выражение, которое может содержать целые числа, переменные n и m, операции сложения (обозначается +), вычитания (обозначается −), умножения (обозначается ∗) и круглые скобки для изменения порядка действий. Запись вида 2n для обозначения произведения числа 2 и переменной n неверная, нужно писать 2 ∗ n. Пример правильного (по форме записи) выражения:
n + (m − 1) ∗ 2
В городе есть n + 1 дорога длины m и m + 1 дорога длины n.
Ответ: (n + 1) ∗ m + (m + 1) ∗ n.
Правильным является любое выражение, эквивалетное данному.
школьный этап
№2.4.
В игре «Камень, ножницы, бумага» двое игроков одновременно показывают при помощи руки один из трёх условных символов – «камень», «ножницы» или «бумага». Игрок выигрывает, если он показал камень, а его противник – ножницы («камень тупит ножницы»), если он показал ножницы, а его противник – бумагу («ножницы режут бумагу»), если он показал бумагу, а его противник – камень («бумага накрывает камень»). Если два игрока показали одинаковые символы, то игра заканчивается вничью. Алёша и Боря сыграли в эту игру девять раз. Алёша два раза показал камень, три раза – ножницы, четыре раза – бумагу. Боря три раза показал камень, четыре раза – ножницы, два раза – бумагу, но порядок, в котором они показывали эти символы, неизвестен. Определите, какое наибольшее число раз мог выиграть Алёша. А какое наибольшее число раз мог выиграть Боря? Объясните свой ответ.
Составим таблицу, сколько раз каждый из мальчиков показывал каждый символ:
| Алёша | Боря | |
|---|---|---|
| Камень | 2 | 3 |
| Ножницы | 3 | 4 |
| Бумага | 4 | 2 |
Боря мог выиграть все 9 раз, если 3 раза Боря показал камень, Алёша – ножницы, 4 раза Боря показал ножницы, Алёша – бумагу, 2 раза Боря показал бумагу, Алёша – камень. Посчитаем, сколько раз Алёша мог выиграть у Бори. Такое могло произойти в следующих случаях:
1) Алёша показывает камень, Боря – ножницы. Это могло произойти не более 2 раз.
2) Алёша показывает ножницы, Боря – бумагу. Это могло произойти не более 2 раз.
3) Алёша показывает бумагу, Боря – камень. Это могло произойти не более 7 раз.
Таким образом, Алёша мог выиграть не более 7 раз. Необходимо также привести пример, когда Алёша выиграл у Бори 7 раз.
1) Алёша показывает камень, Боря показывает ножницы – 2 раза.
2) Алёша показывает ножницы, Боря показывает бумагу – 2 раза.
3) Алёша показывает бумагу, Боря показывает камень – 3 раза.
4) Алёша показывает бумагу, Боря показывает ножницы – 1 раз.
5) Алёша показывает ножницы, Боря показывает ножницы – 1 раз.
Алёша выигрывает в случаях 1-3, то есть 7 раз.
школьный этап
№2.5.
В мастерской по изготовлению матрёшек работают резчики по дереву и художники. Один резчик может за день вырезать пять матрёшек, а один художник за день расписывает две матрёшки. Мастерская получила заказ на изготовление 200 матрёшек, который необходимо выполнить за 20 дней (каждую матрёшку необходимо вырезать и расписать). Какое наименьшее число резчиков и художников должно быть в мастерской, чтобы мастерская успела выполнить заказ вовремя?
За день мастерская должна производить не менее 10 матрешек, поэтому необходимо не менее 2 резчиков и не менее 5 художников. Но при таком количестве резчиков они успевают изготовить 200 матрёшек ровно за 20 дней, и последние изготовленные матрёшки не успеют расписать художники, поэтому должно быть минимум три резчика. Аналогично, художники не смогут приступить к работе немедленно, поэтому на работу художникам также будет отведено менее 20 дней, значит, необходимо минимум 6 художников. 3 резчика изготовят 200 матрёшек за 14 дней, 6 художников распишут 200 матрёшек за 17 дней, поэтому работая одновременно они уложатся в 20 дней.
Ответ: 3 резчика и 6 художников.
школьный этап
№2.6.
Гномы добывают бриллиант для обручального кольца Белоснежки. Им нужно, чтобы он был синий или весил меньше десяти граммов, но при этом чтобы его вес делился на 4 или не делился на 2. Есть ли из найденных гномами бриллиантов подходящие и если да, то какие?
1) синий, 5 граммов;
2) красный, 12 граммов;
3) синий, 12 граммов;
4) синий, 8 граммов;
5) синий, 6 граммов;
6) красный, 7 граммов?
Одновременно должны выполняться 2 условия: синий или меньше десяти граммов и вес делится на 4 или не делится на 2. Первое условие не выполняется в пункте 2 (ни цвет, ни размер не подходят), второе условие не выполняется в пункте 5 (здесь вес 6: он делится на 2, но при этом не делится на 4). Таким образом, все остальные бриллианты – 1, 3, 4 и 6 – подходят.
Ответ: 1, 3, 4, 6.
школьный этап
№3.1.
Составим все возможные последовательности из пяти букв, используя только символы L, R, V, и выпишем их в алфавитном порядке. Вот начало этого списка:
1. LLLLL
2. LLLLR
3. LLLLV
4. LLLRL
Определите последовательности, которые будут идти в этом списке под номерами 8, 81, 98, 110,179.
Возможно, вам будет проще ответить на третий и четвертый вопрос если вы будете знать, что на 100-м месте в этом списке стоит строка RLVLL.
В ответе нужно записать пять строк, состоящих из латинских букв. Ответ на каждое задание нужно писать в отдельной строке (в первой строке — слово, стоящее в списке 8-м, во второй строке — слово, стоящее 81-м, в третьей строке — 98-м, в четвертой строке — 110-м, в пятой строке — 179-м). Порядок записи строк в ответе менять нельзя. В ответе должно быть ровно пять строк. Если вы не можете найти какой-то из ответов, вместо него напишите любую строчку из данных пяти букв.
Такие последовательности связаны с троичной системой счисления. Если заменить букву L на цифру 0, букву R на цифру 1, а букву V на цифру 2, то получится такая последовательность:
00000
00001
00002
00010
То есть в строке номер i записано представление в троичной системе счисления числа i − 1, дополненного нулями до пяти цифр.
Число, стоящее в строке 8, можно получить из числа, стояшего в строке 4, прибавлением 4, то есть при помощи увеличения на 1 двух последних цифр. Получим последовательность LLLVR.
Так как 81 = 34, то первые 81 последовательность начинаются с буквы L, а следующие 4 буквы представляют собой все последовательности длины 4. Последовательность под номером 81 будет последней из них, ответ на этот вопрос — LVVVV.
Для ответа на третий вопрос (что записано в строке 98) можно использовать информацию о том, что в строке 100 записано RLVLL. Для получения ответа нужно уменьшить число на 2. Ответом будет строка RLRVR
Для ответа на четвертый вопрос строку RLVLL нужно увеличить на 10. Ответом будет RRLLR.
Наконец, для ответа на последний вопрос (что записано в строке 179) переведем число 178 в троичную систему счисления. Получится число 20121, поэтому ответом на последний вопрос будет строка VLRVR.
Ответ:
LLLVR
LVVVV
RLRVR
RRLLR
VLRVR
школьный этап
№3.2.
На берегу бурной реки встретились горилла с двумя детьми и шимпанзе с двумя детьми. К берегу прибилось бревно, которое вмещает только двух обезьян, но, во-первых, управлять бревном могут только взрослые особи, а во-вторых, если на бревне или на берегу горилл будет больше, чем шимпанзе, то они их съедят. Как всем обезьянам благополучно переправиться? Запишите алгоритм переправы.
Введём обозначения:
Горилла – взрослая горилла; горилла1 – первый ребенок гориллы, горилла2 – второй ребенок гориллы.
Шимпанзе – взрослая шимпанзе; шимпанзе1 – первый ребенок шимпанзе, шимпанзе2 – второй ребенок шимпанзе.
Алгоритм:
1. Переправить Горилла и горилла1
2. Переправить Горилла
3. Переправить Горилла и горилла2
4. Переправить Горилла
5. Переправить Шимпанзе и шимпанзе1
6. Переправить Шимпанзе и горилла2
7. Переправить Шимпанзе и Горилла
8. Переправить Шимпанзе и горилла1
9. Переправить Шимпанзе и шимпанзе2
10. Переправить Горилла
11. Переправить Горилла и горилла1
12. Переправить Горилла
13. Переправить Горилла и горилла2
школьный этап
№3.3.
Робинзон Крузо живёт на острове с двумя племенами, представители одного из них лгут по понедельникам, вторникам и средам, другого – по четвергам, пятницам и субботам, в остальные дни все говорят правду. Робинзон не умеет отличать представителей двух племен, но знает, что они вступают в брак только с представителями другого племени. Однажды Робинзон встретил супружескую пару, и муж сказал: «Завтра я буду лгать». А жена: «А я лгала вчера и буду лгать завтра». Помогите Робинзону узнать, какой сейчас день недели. (Укажите и обоснуйте ваш ответ.)
Жена не может говорить правду, так как нет такого дня, чтобы он был правдив, а оба рядом -- лживые, ни для одного племени. Значит, она лжет, а муж говорит правду. Но так как сегодня не воскресенье (тогда оба говорили бы правду), то это среда. Действительно, тогда жена лгала вчера, а завтра не лжет.
Ответ: Среда.
школьный этап
№3.4.
Три вора – Камнев, Ножницын и Бумагин хотят переправиться через реку. У каждого вора два больших баула. В лодке три места, одно место занимает один человек или один баул. Грести умеет только Камнев. При этом если Камнев останется в лодке или на берегу с баулом Ножницына и Ножницына не будет рядом, то Камнев обчистит баул Ножницына. Аналогично Ножницын обчистит баул Бумагина в его отсутствие, а Бумагин обчистит баул Каменева в его отсутствие. Как им переправиться на другой берег? Опишите алгоритм их действий.
Возможный алгоритм действий.
1) Камнев перевозит два своих баула и возвращается назад.
2) Камнев перевозит Ножницына с баулом Ножницына, возвращается с Ножницыном.
3) Камнев перевозит Ножницына с баулом Ножницына, возвращается один назад.
4) Камнев перевозит Бумагина с баулом Бумагина, оставляет их на другом берегу, возвращается назад с двумя своими баулами.
5) Камнев перевозит баул Бумагина и возвращается назад.
6) Камнев перевозит два своих баула.
школьный этап
№3.5.
К реке подошли Волчица с двумя волчатами и Лисица с двумя лисятами. У берега привязана лодка, которая вмещает только двух зверей. Ситуация осложняется тем, что Волчица с Лисицей не доверяют друг другу и не оставят своих детей в своё отсутствие с другой мамой ни на берегу, ни в лодке. Грести умеют только Лисица и один из лисят. Как им переправиться?
Обозначим лисенка, который умеет грести как «лисенок1». Возможный план перевозки.
1. Перевезти лисенка1 и лисенка.
2. Перевезти лесенка1
3. Перевезти Лисицу и лисенка1
4. Перевезти Лисицу
5. Перевезти Лисицу и Волчицу
6. Перевезти лисенка1
7. Перевезти лисенка1 и волчонка
8. Перевезти лисенка1
9. Перевезти лисенка1 и волчонка
школьный этап
№3.6.
Перед Архимедом в ряд положили четыре одинаковые с виду монеты. Среди них обязательно есть как золотые, так и серебряные в позолоте (легче золотых). Известно, что любая золотая монета лежит правее любой серебряной. Как Архимеду за одно взвешивание на чашечных весах без гирь определить тип каждой монеты, лежащей на столе?
Так как золотые точно есть, то самая правая – золотая. Аналогично, самая левая – серебряная. Теперь взвесим первую и четвёртую монету со второй и третьей. Если весы в равновесии, значит посередине лежат золотая и серебряная монеты. Если первая и четвёртая перевешивают, значит посередине две серебряных. Если перевешивают вторая и третья, значит посередине две золотых.
школьный этап
№4.1.
На трёх путях сортировочной станции стоят вагоны с абрикосами (А), бананами (Б) и вишней (В) так, как это показано на рисунке.

Машинист тепловоза (Т) может за один раз прицепить к тепловозу один или несколько вагонов с какого-нибудь пути, передвинуть их на правый путь, после чего передвинуть их на любой левый путь. Например, если тепловоз заберет 2 вагона с пути номер 3 на путь номер 1, то после такого действия распределение вагонов по путям будет таким.
1. А В Б А В
2. Б В А
3. Б
Соответствующую команду перемещения будем записывать так.
2 3 1
Что означает, что необходимо передвинуть 2 вагона с пути номер 3 на путь номер 1. Первое число обозначает количество перемещаемых вагонов, второе число — номер пути, с которого нужно забрать вагоны, третье число — номер пути, на который нужно передвинуть вагоны. Разработайте алгоритм действий машиниста, необходимых для того, чтобы сформировать на каждом из путей составы с одинаковыми фруктами (не важно, на каком именно пути). Алгоритм оформите в виде последовательности команд, записанных в отдельных строках. Каждая команда имеет указанный выше вид: сначала записано число передвигаемых вагонов, потом номер пути с которого передвигаются вагоны, затем номер пути, на который передвигаются вагоны.
Например, следующая запись:
2 3 1
1 2 3
означает “передвинуть 2 вагона с пути 3 на путь 1, затем передвинуть 1 вагон с пути 2 на путь 3”. Чем меньше команд будет в вашем алгоритме, тем большее количество баллов вы получите.
Самое короткое решение состоит из 7 команд:
2 1 3
4 3 2
5 2 1
3 1 2
1 3 2
5 2 3
2 3 2
Это решение оценивается в 10 баллов. Более длинные решения оцениваются меньшим числом баллов.
школьный этап
№4.2.
По столбу высотой 1 метр ползут две неутомимые улитки. Движутся они равномерно. Первая улитка в первую половину суток (период с 00:00 до 12:00) сползает на 30 см, а во вторую половину суток (период с 12:00 до 00:00) поднимается на 50 см. Вторая улитка в период с 00:00 до 12:00 сползает на 5 см, а в период с 12:00 до 00:00 поднимается на 30 см. Какая улитка, первая или вторая, доберётся до верхушки столба раньше, и когда это произойдёт, если они начали ползти от основания столба в понедельник в 12:00? Объясните полученный ответ.
Первая улитка достигнет отметки в 60 сантиметров за 72 часа (четверг 12:00). Учитывая
равномерность передвижения, последние 40 сантиметров первая улитка проползет за 9 часов
36 минут, т.е. достигнет верхушки столба в четверг в 21:36. (Общее время в пути – 81 час 36
минут).
Вторая улитка за 72 часа (четверг 12:00) достигнет отметки в 75 сантиметров. За следующие
10 часов (четверг 22:00) она проползет 25 сантиметров и достигнет отметки 1 метр. (Общее
время второй улитки 82 часа).
Таким образом, первая улитка достигнет верхушки столба раньше второй улитки, и это
произойдёт в четверг в 21:36.
школьный этап
№4.3.
Семья рыбаков (отец и сын) хочет переправить боевую группу из 6 бойцов на Тайный остров архипелага в тылу врага. Есть двухместная лодка. Не запомнив дороги, без проводника её не проплыть. Вначале дорогу до Тайного острова знает только рыбак-отец. Но всех проводить он не сможет: путь лежит мимо Сторожевой башни, и каждый из них может проплыть мимо неё не более 5 раз в любом направлении (иначе поднимется тревога). Остальные могут стать проводниками, запомнив дорогу. Рыбак-сын запоминает дорогу, если проплыл по ней один раз, а бойцу для этого надо проплыть туда и обратно. В конце все рыбаки должны быть дома, все бойцы – на острове, лодка – где угодно. Запишите алгоритм переправы.
1. Переправить Отца и Бойца 1.
2. Отец и Боец 1 возвращаются (Боец 1 запомнил дорогу).
3. Переправить Отца и Сына (Сын запомнил дорогу).
4. Отец возвращается.
5. Переправить Бойца 1 и Бойца 2.
6. Сын и Боец 2 возвращаются (Боец 2 запомнил дорогу).
7. Переправить Сына и Бойца 3.
8. Сын возвращается.
9. Переправить Бойца 2 и Бойца 4.
10. Боец 2 возвращается.
11. Переправить Бойца 2 и Бойца 5
12. Боец 1 возвращается
13. Переправить Бойца 1 и Бойца 6.
школьный этап
№4.4.
Есть чашечные весы без делений. Для взвешивания груза также можно использовать гирьки, массы которых – целое число граммов. Вам необходимо предложить набор гирек, при помощи которого можно отмерить на весах любую массу, равную целому числу граммов от 1 до 20, при этом число гирек в наборе должно быть как можно меньше. Гирьки можно класть на каждую чашку весов, чашки весов должны находиться в равновесии, при этом на одной из чашек весов должен находиться взвешиваемый груз. Массы гирек в наборе могут повторяться. Объясните, как любую массу от 1 до 20 граммов можно взвесить при помощи предложенного набора.
В оптимальном наборе гирек для уравновешивания любых масс необходимо использовать гирьки, массы которых являются степенями тройки: 1, 3, 9, 27 и т. д. Это связано с тем, что любое число можно представить в уравновешенной троичной системе счисления, при этом цифра 1 будет соответствовать тому, что гирька данной массы кладётся на одну чашку весов, цифра −1 будет соответствовать гирьке на другой чашке весов, а 0 означает, что данная гирька не используется.
Приведем пример уравновешивания всех масс от 1 до 20 при помощи гирек массами 1, 3, 9, 27.
1 = 1.
2 = 3 − 1,
3 = 3,
4 = 3 + 1,
5 = 9 − 3 − 1,
6 = 9 − 3,
7 = 9 − 3 + 1,
8 = 9 − 1,
9 = 9,
10 = 9 + 1,
11 = 9 + 3 − 1,
12 = 9 + 3,
13 = 9 + 3 + 1,
14 = 27 − 9 − 3 − 1,
15 = 27 − 9 − 3,
16 = 27 − 9 − 3 + 1,
17 = 27 − 9 − 1,
18 = 27 − 9,
19 = 27 − 9 + 1,
20 = 27 − 9 + 3 − 1.
От учащегося требуется привести пример конструкции из трёх гирек (их массы могут отличаться от примера 1, 3, 9, 27) и показать, что любую массу можно уравновесить при помощи данного набора гирек.
школьный этап
№4.5.
Серёжа, Костя и Женя решили помочь малышам построить замок из цветных кубиков. Кубиков всего девять: три красных, три жёлтых и три синих. Замок состоит из трёх башен следующей формы и цветов.

Мальчики договорились, что в их бригаде каждый может ставить только кубики одного цвета: Серёжа ставит синие кубики, Костя – красные, Женя – жёлтые. Каждую секунду каждый из мальчиков может выполнить только одно из трёх действий.
• Взять кубик.
• Поставить кубик на место.
• Ничего не делать.
При этом одновременно мальчики не могут ставить кубики в одну и ту же башню. Сколько секунд понадобится Серёже, Косте и Жене, чтобы построить замок? Запишите алгоритм их действий.
Запишем решение в виде таблицы, в которой указаны действия каждого мальчика в каждую секунду. Запись «+С» означает, что мальчик берёт в руку синий кубик, запись «С1», «С2», «С3» означает, что мальчик ставит синий кубик в первую, вторую или третью башню. Буква «К» обозначает красный цвет, «Ж» – жёлтый. Наилучшее решение возможно за 9 секунд.

Другие решения требуют большего времени. В приведённом выше решении используется «оптимизация» – когда один мальчик кладёт кубик, то другой одновременно берёт кубик в руку и кладёт его в следующую секунду. Это позволяет положить два первых кубика в первую башню за три секунды. Если не использовать такую оптимизацию, то есть если мальчики одновременно берут кубики в руку на нечётных секундах и ставят кубики в башни на чётных секундах, то решение возможно только за 10 секунд.
школьный этап
№4.6.
Трём англичанам, путешествующим в джунглях Африки, и трём их проводникам из местного племени требуется переправиться на противоположный берег реки. В распоряжении путешественников имеется небольшая надувная лодка, способная вместить только двух человек. Англичане подозревают, что проводники – из племени людоедов, и чувствуют себя в опасности всегда, когда находятся в меньшинстве. Как устроить безопасную переправу?
Возможный план перевозки:
1. Перевезти двух проводников.
2. Один проводник возвращается обратно.
3. Перевезти двух проводников.
4. Один проводник возвращается обратно.
5. Перевезти двух англичан.
6. Англичанин и проводник возвращаются обратно.
7. Перевезти двух англичан.
8. Один проводник возвращается обратно.
9. Перевезти двух проводников.
10. Один проводник возвращается обратно.
11. Перевезти двух проводников.