Отношения объектов и их множеств
Различные объекты могут иметь отношения между собой.
Пример:
» Останкинская телебашня находится в Москве;
» Один байт равен восьми битам;
» Лёша – брат Артёма и сын Ивана.
| Отношение – это взаимная связь между множествами.
Пример.
Между городами А, Б, В, Г проложены автомобиль-ные дороги. Город А имеет сообщение с городами В, Г, город Б – с городом Г, город В – с городами А, Г.
Изобразим отношение между этими множествами наглядно:
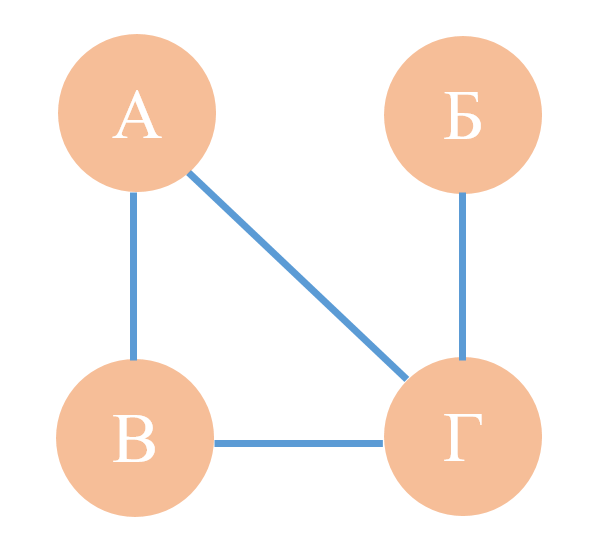
Некоторые отношения изменяют порядок своего по-ложения в зависимости от условия. Такие отношения обозначают стрелкой.
Пример.
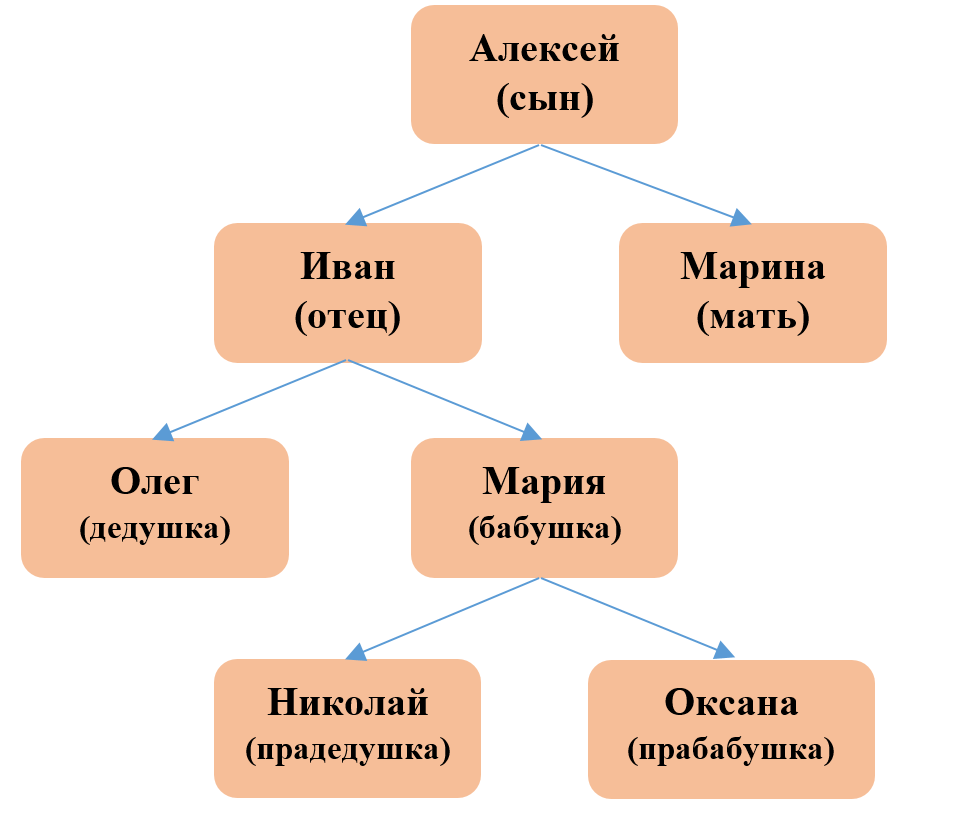
Отношения между множествами
Отношения могут связывать множества объектов.
Для удобного представления таких отношений используют диаграммы Эйлера-Венна.
✒ Определение: Если множества А и В имеют общие элементы, то такие множества пересекаются.
Пример.
Пусть А – множество интернет магазинов, В – множество всех магазинов одежды. В пересечение этих множеств попадают все интернет магазины одежды.
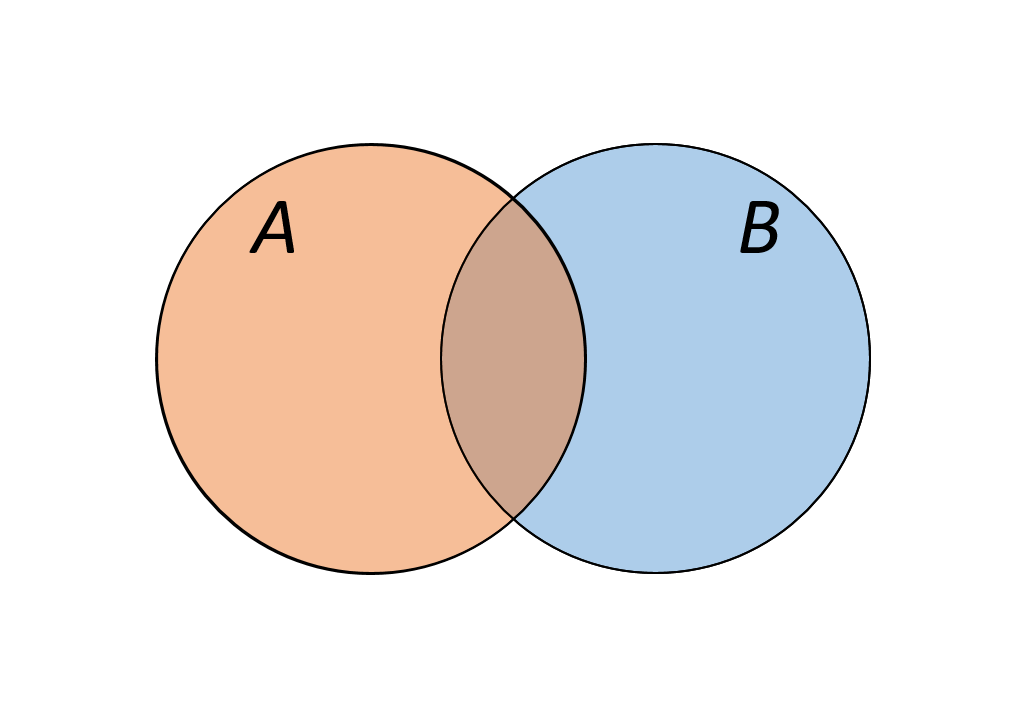
✒ Определение: Если множества не имеют общих элементов, то такие множества не пересекаются.
Пример.
Пусть А – множество паровых двигателей, В – множество книг по биологии. Эти множества не имеют общих элементов.
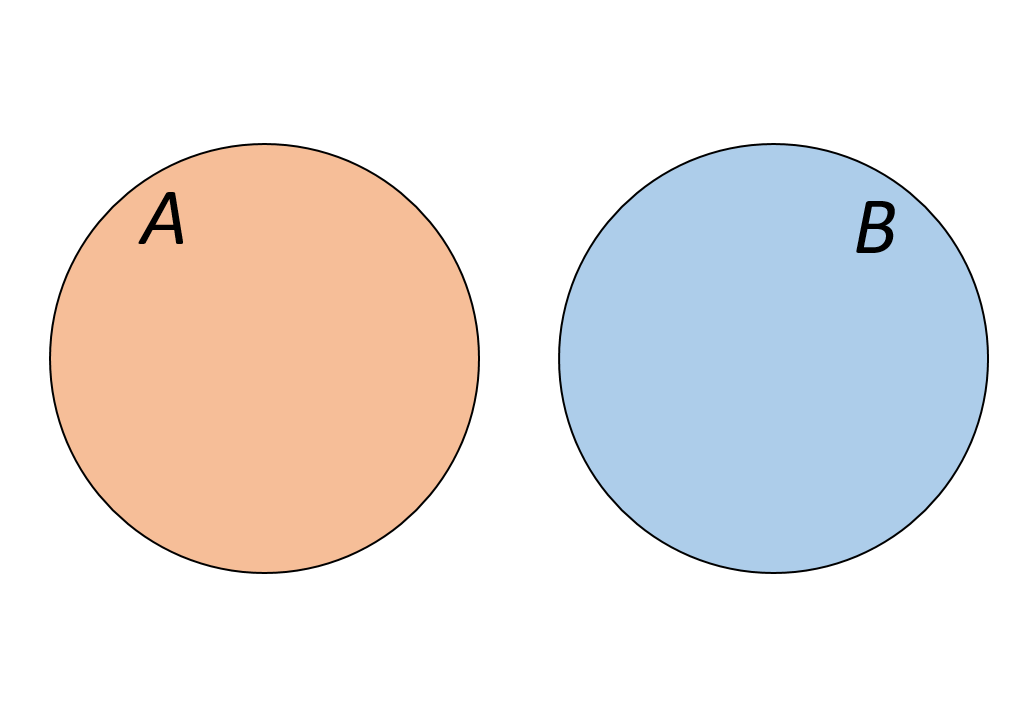
✒ Определение: Если каждый элемент В входит в множество А, то множество В – подмножество А.
Пример.
Пусть А – множество литературных персонажей, В – множество героев романа Гарри Поттер. Множество героев романа является подмножеством множества литературных персонажей.
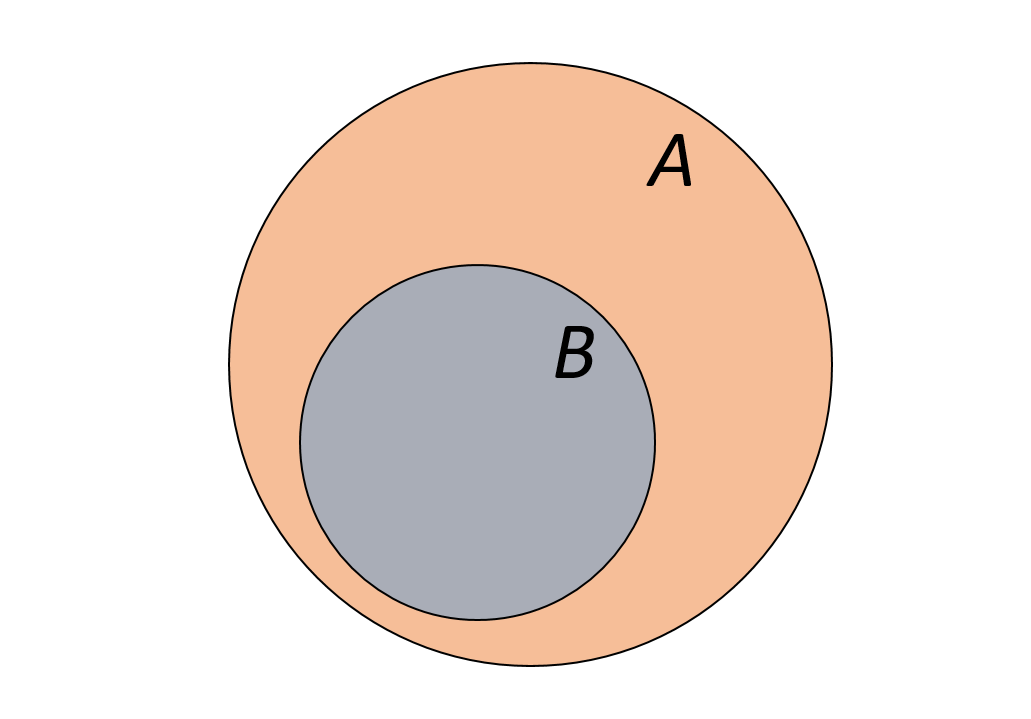
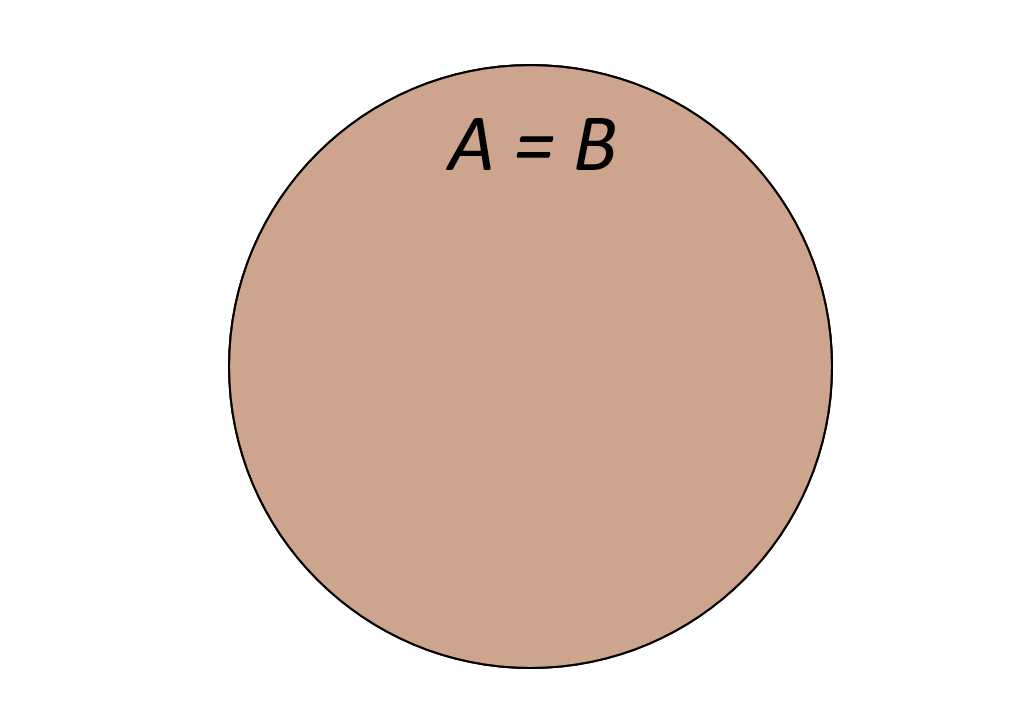
✒ Определение: Если каждый элемент множества В является элементом множества А и, на оборот, то множества А и В равны.
Пример.
Пусть А – множество равносторонних прямоугольников, В – множество квадратов. Эти множества являются равными.
Литература:
1. Информатика: учебник для 6 класса / Л.Л. Босова, А.Ю. Босова. - М.: БИНОМ.Лаборатория знаний, 2016. - 244 с.
Задачи на диаграммы Эйлер-Венна.
Задача №1.
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. Сколько шестиклассников являются читателями обеих библиотек?
Решение:
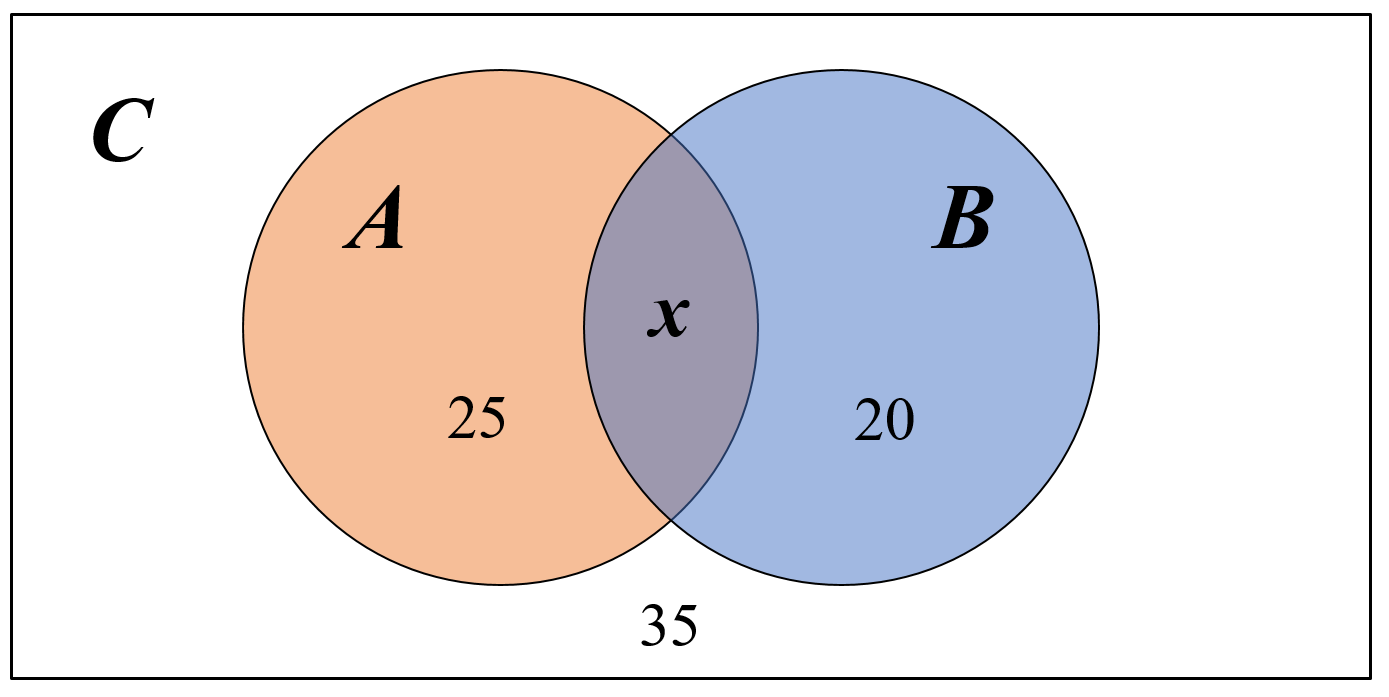
А– посещающие школьную библиотеку (25);
B– посещающие районную библиотеку (20);
С– общее количество шестиклассников (35);
Обозначим за x – количество шестиклассников, посещающих обе библиотеке.
25 + 20 – х = 35
45 – х = 35
х = 45 – 35
х = 10
Ответ: 10 человек являются читателями обоих библиотеки.
Задача №2.
В классе 25 учащихся. Из них 5 человек не умеют играть на в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 – в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?
Задача №3.
В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
а) пересечении;
б) объединении?
Задача №4.
Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский изучают 25 человек, французский – 27 человек, а тот и другой 18 человек. Сколько всего учеников в классе?
Задача №5.
В детском саду 52 ребёнка. Каждый из них любит либо пирожное, либо мороженое, либо и то и другое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любят мороженое?
Задача №6.
В классе 35 учеников, каждый из них любит футбол, волейбол или баскетбол, а некоторые – два или даже три из этих видов спорта. 24 ученика любят футбол, 18 – волейбол, 12 баскетбол. При этом 10 учеников одновременно любят футбол и волейбол, 8 – футбол и баскетбол, а 5 – волейбол и баскетбол. Сколько учеников этого класса любят все три вида спорта.
